Selamat pagi para pembaca yang rajin belajar, kali ini kita belajar tentang bilangan bulat dan pecahan. Bilangan bulat adalah salah satu dari beberapa jenis bilangan yang ada dalam ilmu Matematika.
Bilangan Bulat
Bilangan bulat ada tiga jenis yaitu nol, bilangan bulat negatif dan bilangan bulat positif. Dalam istilah Matematika dapat disebutkan bahwa bilangan bulat itu adalah 0, >0 dan <0.
Perhatikan contoh gambar bilangan bulat dibawah ini agar kalian lebih cepat paham.
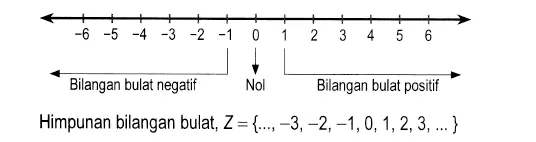
Berdasarkan denah diatas, himpunan bilangan bulat, Z= {….,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,…}
Tanda …. diatas menandakan bahwa terus hingga infinitif atau tidak terbatas.
Operasi Hitung Bilangan Bulat
Dalam ilmu matematika dasar, kita mengenal operasi hitung bilangan bulat. Operasi hitung bilangan bulat seperti:
- Penambahan bilangan bulat
- Pengurangan bilangan bulat
- Perkalian bilangan bulat
- Pembagian bilangan bulat
Keempatnya juga disebut operator dasar dalam Matematika.
Penjelasan dan contoh operasi hitung diatas dapat anda lihat dibawah ini.
Penambahan Bilangan Bulat
Dalam operasi hitung ini, ada tiga situasi yang mungkin terjadi yaitu:
- Penambahan dua bilangan bulat positif
- Penambahan dua bilangan bulat negatif
- Penambahan dua bilangan bulat positif dan negatif
- Penambahan Dua bilangan Positif
Ketika adik adik menemukan perhitungan atau soal soal yang menunjukkan operasi hitung penambahan dan semua nilai yang tertuang dalam soal tersebut adalah bilangan bulat positif. Hal tersebut dapat anda lihat dengan tidak adanya lambang negatif (-) pada soal tersebut atau bagian soal yang anda ingin kerjakan.
Artinya aturan dari perhitungan tersebut adalah nilai bilangan akan semakin besar atau berdasarkan sumbu x, akan semakin ke kanan dari posisi nol, dan untuk sumbu y akan semakin ke atas (dari posisi nol). Hal tersebut dapat lihat pada contoh soal dan diagram bilangan bulat dibawah ini.
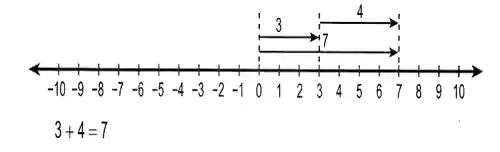
Jadi hasil penambahan dari: 3 + 4 = 7. Kalian juga dapat menambahkan dua jenis atau bahkan sepuluh jenis bilangan bulat, dan yang terjadi adalah nilainya akan semakin bertambah besar. Apalagi bilangan bulat positif yang tidak berbentuk pecahan.
Penambahan Dua Bilangan Bulat Negatif
Penambahan bilangan bulat yang kedua adalah operasi hitung dua bilangan bulat negatif. Jadi, berbeda dengan yang sebelumnya diatas, operasi hitung ini adalah menambahkan dua bilangan negatif. Artinya, dua bilangan atau lebih tersebut berada di sisi kiri 0 pada sumbu X atau sisi bawah 0 pada sumbu Y. Perhatikan contoh soal penambahan dua bilangan negatif dibawah ini.
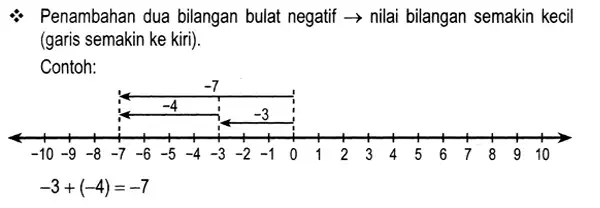
Nah, jadi kalo adik adik diberikan soal operasi hitung bilangan bulat yang mengharuskan adik adik untuk menambah dua atau bahkan sepuluh nilai matematis, semakin besar angkanya, semakin menjauh ke kiri dari 0 sumbu X atau menjadi semakin besar angka negatif nya. Sebagai contoh:
-5+-5+-4+-3+-20+-23= -60
Perhitungan diatas kita dapat bentuk menjadi lebih sederhana menjadi
-5+(-5)+(-4)+(-3)+(-20)+(-23)=-5-5-4-3-20-23=-60
Kok bisa seperti itu? Nah, kalian masih ingat tidak aturan ketika simbol positif bertemu dengan tanda kurung yang berisikan simbol negatif. Tentu saja akan terjadi operasi perkalian, dan hasilnya akan berubah menjadi negatif. Berbeda ketika simbol negatif dikalikan dengan simbol negatif, hasilnya menjadi positif. Kalian dapat mempelajari lebih banyak pad contoh soal nanti diakhir postingan.
Penambahan Bilangan Bulat positif dan Negatif
Selanjutnya adalah penambahan satu bilangan positif dan satu bilangan negatif. Hasil dari operasi hitung seperti ini akan sangat bergantung dengan nilai atau nominal angka yang dihitung. Ketika angka bilangan positif lebih banyak maka nilai angka tersebut pasti pada sisi kanan 0 sumbu X atau sisi atas 0 sumbu Y. Sebaliknya terjadi ketika angka bilangan positif lebih besar.
Perhatikan contoh soal dibawah ini dan grafiknya.
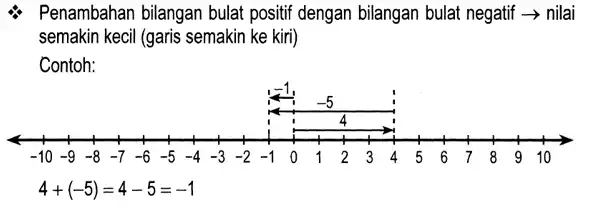
Hal yang sama pun terjadi ketika adik adik diberikan soal yang mempunyai banyak angka penambahan bilangan bulat positif dan negatif. Pertama adik adik dapat membaginya dua dua bagian, ataupun langsung menghitung secara keseluruhan.
Pada dasarnya penjumlahan yang terjadi antara bilangan bulat positif dan bilangan bulat negatif sama saja dengan mengurangi angka atau bilangan yang pertama atau mempunyai hirarki hitung yang tertinggi. Contoh soal dibawah ini
10 + -20 + -20 + 40 + -10 + 30 = ?
Kita dapat membaginya menjadi dua dua menggunakan tanda kurung, atau langsung hitung secara keseluruhan mulai dari angka pertama
10 + -20 + -20 + 40 + -10 + 30 =(10 +-20) + (-20 + 40) + (-10+30) = (10-20) + (-20+40) + (-10+30) = (-10) + (20) + ( 20) = 30
Nah mudah bukan. Kalian pun bisa langsung menghitungnya yaitu menggunakan pikiran. Jadi otak kalian itu seperti melakukan proses perhitungan langsung. 10 +-20 artinya -10, lalu -10 + -20 artinya -30, kemudian di tambah 40 artinya 10, lalu ditambah -10 artinya 0, dan akhirnya ditambah 30 artinya sama dengan 30.
Bila kalian sudah mengusai cara berhitung seperti diatas yang langsung, maka dijamin adik adik dapat mengerjakan soal lebih cepat dan lebih mahir. Bahkan tanpa tips dan trik cepat kerja soal pun adik adik pasti mampu mengerjakan soal ujian semester ataupun ujian akhir sekolah dengan sangat cepat.
Bagi yang belum bisa dengan cepat, silahkan tambah kecepatan adik adik dengan latihan soal terus menerus. Ketika anda telah latihan selama 20 jam total dalam menghitung menambahkan angka bilangan 2 atau 3 digit (puluhan atau ratusan) , saya jamin kecepatan tersebut akan meningkat drastis.
Hal ini dapat kalian buktikan pada teman teman kelas kalian yang sudah berpengalaman jaga toko. Apalgi teman kalian yang etnis Tionghoa yang sering jaga toko. Mereka sangat cepat dalam operasi hitung tambah dan kurang karena hal ini.
Pengurangan Bilangan Bulat
Oke, sekarang kita bahas operasi hitung selanjutnya dalam bilangan bulat yaitu pengurangan bilangan bulat. Sama halnya dengan bagian penambahan diatas, dalam operasi ini juga terdiri atas tiga bagian yaitu:
- Pengurangan dua bilangan bulat positif
- Pengurangan dua bilangan bulat negatif
- Pengurangan bilangan bulat positif dan negatif
Berikut penjelasan dan contoh ketiga jenis operasi hitung pengurangan bilangan bulat diatas.
Pengurangan Dua Bilangan Bulat Positif
Ketika terdapat soal yang menuliskan tentang operasi hitung pengurangan dua bilangan positif, artinya operasi tersebut sama saja dengan mengharuskan kita mengurangi angka pertama yang dituliskan. Biasanya urutannya dimulai dari sisi kiri perhitungan, atau sesuai hirarki operasi hitung.
Perhatikan contoh dibawah ini agar lebih mengerti:
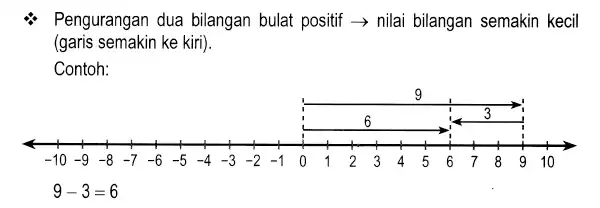
Artinya, nilai total angka bilangan bulat yang dihasilkan akan selalu lebih kecil dari angka bilangan tersebut. Mau yang kanan yang besar ataupun yang kiri, hasilnya tetap akan membuatnya angkanya lebih kecil.
Note: Dalam mengerjakan soal dalam operasi hitung pengurangan dua bilangan positif, hati hati membolak balik urutan soal karena dapat mengubah nilai akhir
Lihat saja contoh diatas, bila kita memutar penulisannya dari 9-3 menjadi 3-9 maka akan mengubah nilainya menjadi -6. Ingat bahwa dalam perhitungan diatas sesungguhnya ada tanda kurung pada angka tiga yang memisahkannya dengan operasi hitung kurang (-). Seperti in: 9-(3) = 9-3 = 6. Jadi awalnya bukan “sembilan minus tiga” tapi “positif sembilan kurang positif tiga” yang kemudian menjadi “sembilan minus tiga”.
Pengurangan Dua Bilangan Bulat Negatif
Ketika adik adik menemukan soal operasi hitung pengurangan dua atau lebih bilangan negatif, maka adik adik harus memahami bahwa operasi hitung pengurangan akan berubah menjadi penambahan akibat dikalikan dengan simbol negatif pada angka bilangan bulat negatif.
Perhatikan contoh soal dibawah ini dan diagramnya.
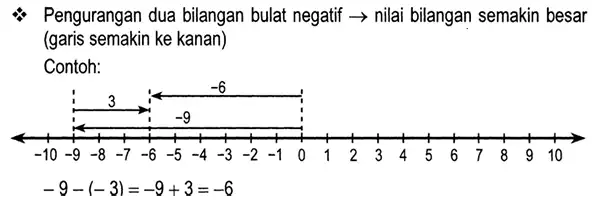
Dapat anda amati bahwa soal diatas, adalah -9-(-3) = -9 + 3 = -6. Artinya untuk semua perhitungan yang terjadi dalam operasi perhitungan seperti ini, akan mengakibatkan bertambah kecilnya angka bilangan negatif yang ada. Dan bahkan hasil akhirnya dapat merupakan bilangan positif. Contoh soal seperti -9 – (-30) = 21. Ada banyak lagi contoh soal seperti ini.
Pengurangan Bilangan Bulat Positif dan Negatif
Ketika ada soal seperti ini, mudah saja, sisa kalian jawab sesuai urutan hirarki hitung yang ada. Bila hanya ada operasi hitung pengurangan, maka hitung dari paling kiri. Lihat contoh dibawah ini:
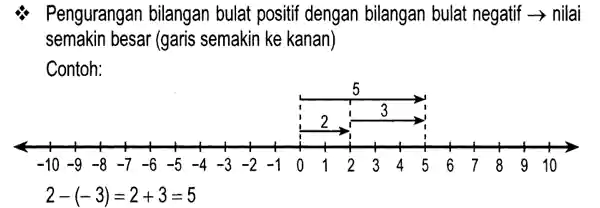
Dapat anda lihat bahwa soal adalah 2 – (-3) = 2 + 3 = 5. Ketika anda balik urutannya maka dari awal dan tetap mempertahankan operasi hitung maka hasilnya akan salah. Lihat saja: (-3) – 2 = -5. Berbeda bukan. Harusya ketika anda ingin mengubah urutannya, anda membaliknya ketika semua simbol yang ganda seperti pada: – (-3) ini.
Selanjutnya adalah bagian perkalian dan pembagian bilangan bulat.
Perkalian dan Pembagian Bilangan Bulat
Dalam operasi hitung yang lebih tinggi hirarkinya dari penjumlahan dan pengurangan yaitu perkalian, adik adik harus mengikuti aturan yang ada dibawah ini. Ingat harus dihapal aturan dibawah ini dan dihayati dengan sebaik baiknya.
Bilangan bertanda sama sama, atau Bilangan positif dan positif ataupun bilangan negatif dan negatif ketika dalam operasi perkalian dan atau pembagian pasti menghasilkan bilangan bernilai positif atau bilangan bulat positif (+)
Bilangan berbeda tanda atau bilangan positif dan bilangan negatif dalam operasi perkalian dan atau pembagian pasti menghasilkan bilangan bulat negatif (-).
Pertanyaan diatas adalah mutlak. Makanya harus anda ingat. Sebelumnya diatas saya menyebutkan bahwa adanya perubahan ketika operasi pengurangan ataupun penambahan akan berubah ketika bertemu tanda kurung sesuai dengan simbolnya. Hal tersebut mengacu pada aturan diatas. Jadi ketika simbol pengurangan bertemu dengan tanda kurung yang berisi angka negatif maka akan menjadi positif sehingga menjadi operasi penambahan (+).
Sebagai contoh:
- 4 x 5 = 20
- 4 x -5 = -20
- 5 x -4 = -20
- 5 x 4 = 20
- 20 : 4 = 5
- 20 : -4 = -5
- 20 : -5 = -4
- -20:-4=5
- -20:-5=4
Operasi Hitung Bilangan Bulat
Diatas, saya berulang ulang menyebutkan tentang hirarki operasi hitung bilangan bulat. Hirarki adalah tingkatan, dalam hal operasi hitung artinya urutan yang paling utama dan paling pertama hingga terakhir dikerjakan atau dihitung dalam suatu operasi hitung. Dibawah ini adalah tabel hirarki operasi hitung bilangan bulat.

Perhitungan tetap seperti biasanya yaitu mulai dari kiri ke kanan ketika hierarki tanda operasi sama dalam soal tersebut.
Kenapa Hirarki Operasi Hitung Penting
Hirarki dalam operasi hitung sangatlah penting karena ketika kita tidak mengikutinya, dapat dipastikan 100 persen perhitungan kita akan salah. Tujuan kita memberikan kurung dalam suatu perhitungan tentu saja selain untuk memisahkannya dengan operasi hitung lainnya tetapi juga untuk membuatnya lebih dahulu harus dihitung.
Begitu juga dengan operasi hitung pangkat dan akar pangkat. Bayangkan perbedaan hasilnya ketika kita ingin menambahkan: 22 + 2 = ?, tentu saja ketika kita tidak memperhatikan hirarki maka kita langsung saja menambahkan dan kemudian mengkuadrakan yang akhirnya bernilai salah. Harusnya seperti ini: 22 + 2 = 4 + 2 = 6.
Kalian dapat lebih mengerti tentang hirarki operasi hitungan bilangan bulat diatas dengan menghafalkan dan memahami sifat sifat bilangan bulat dibawah ini.
Sifat Sifat Bilangan Bulat
- Sifat Komutatif
- Sifat Asosiatif
- Sifat Distributif
- Tertutup
- Mempunyai invers
- Identitas
6 Item diatas adalah hal hal yang perlu kalian hafalkan dan pahami dengan benar untuk mampu meningkatkan skor matematika kalian sekaligus mampu menghitung dengan cepat dan tentunya dengan benar. Berikut contoh dan penjelasannya masing masing
1. Sifat Komutatif
Apa itu sifat komutatif? Pengertian sifat komunitatif adalah keadaan yang dapat dirubah susunannya. Sehingga ketika kita harus menambahkan angka a dan b, anda dapat menuliskan a terlebih dahulu ataupun b terlebih dahulu. Tidak ada masalah di dalamnya. Ada dua kasus atau kejadian dimana sifat komutatif berlaku dalam yaitu:
(1) a + b = b + a
(2) a x b = b x a
Ingat, a dan b dapat berupa bilangan positif ataupun negatif. Terkhusus bilangan negatif, harus diberi dalam kurung. Contoh a = (-2) dan b= (-3), ketika sudah begitu kalian dapat berlakukan sifat komutatif.
Perhatikan bahwa pada dua sifat komutatif diatas hanya ada penambahan dan perkalian, dan tidak ada pembagian dan pengurangan. Hal tersebut tentu saja karena pembagian akan mempunyai nilai yang berbeda ketika dibalik atau diubah posisinya.
2. Sifat Asosiatif
Apa itu sifat asosiatif? Pengertian asosiatif adalah kesamaan hubungan antara variabel yang satu dengan yang lainnya dalam operasi hitung tersebut. Batasan sifat asosiatif dapat adik adik lihat dibawah ini:
(a + b) + c = a + (b + c)
(a x b) x c = a x (b x c)
Ketika kalian mengisikan variabel a, b, dan c dengan bilangan bulat semau kalian (untuk bilangan negatif berikan kurung; contoh (-2)) maka hasilnya pasti akan sama ketika di berikan sifat asosiasi ketika susunan seperti diatas. Contoh
(2 + 3) + 4 = 2 + (3 + 4)
(2 x 3) x 4 = 2 x (3 x 4)
((-2) + 3) + 4 =(-2) + (3 + 4)
(2 x 3) x 4 = 2 x (3 x 4)
Pasti hasilnya akan sama.
3. Sifat Distributif
Apa itu sifat distributif? Pengertian sifat distributif adalah sifat dalam operasi hitung hanya ada dalam operasi perkalian yang bertemu dengan tanda kurung yang berisikan operasi penambahan atau pengurangan. Dibawah ini adalah rumusan sifat distributif dalam perhitungan:
(a +- b) x c = (a x c) +- (b x c)
a x (b +-c) = (a x b) +- (a x c)
Sifat distributif diatas sangat berguna ketika kita ingin menyederhakan suatu persamaan dan juga banyak lagi kegunaannya dalam perhitungan matematis kedepannya.
4. Tertutup
Sifat tertutup adalah batasan mutlak atau ketentuan mutlak yang pasti terjadi. Berikut sifat tertutup tersebut.
Untuk a dan b adalah bilangan bulat, maka hasil pertambahan atau pengurangannya adalah suatu bilangan bulat a +- b = c
Untuk a dan b bilangan bulat, maka hasil perkaliannya adalah suatu bilangan bulat a x b = c
5. Mempunyai invers
Suatu perhitungan dikatakan mempunyai invers ketika perhitungan tersebut mempunyai bentuk seperti dibawah ini.
a + (-a) = (-a) + a = 0
a x 1/a = 1/a x a
6. Identitas
Dalam sifat bilangan bulat, ada dua faktor identitas yang kita ketahui yaitu angka 0 untuk identitas penjumlahan dan angka 1 sebagai identitas perkalian. Berikut rumusan sifat identitas bilangan bulat tersebut:
a + 0 = 0 + a = a; 0 adalah faktor identitas pada operasi penjumlahan
a x 1 = 1 x a = a ; 1 adalah faktor identitas pada operasi perkalian
Contoh Soal
Hasil dari 25 + (-10) – (-30) adalah?
Penyelesaian:
Merupakan operasi penjumlahan dan pengurangan saja, sehingga yang pertama perlu dilakukan adalah mengeluarkan angka dari tanda kurung dengan mengalikan operator nya seperti simbol + dan -.
Ingat aturan perkalian dan pembagian untuk operator positif dan negatif yang ada dibagian perkalian dan pembagian. Atau baca artikel ini untuk lebih jelasnya tentang operator aritmatika.
25 + (-10) – (-30) = 25 – 10 + 30 = 45
Hasil dari -125 x (- 8) adalah …
Penyelesaian:
Merupakan soal perkalian dua bilangan bulat negatif. Sangat mudah. Artinya, berdasarkan aturan perkalian dua bilangan bulat negatif yang telah dijelaskan dibagian atas, hasilnya pasti bilangan bulat positif.
-125 x (-8) = -125 x -8 = 1000
Hasil dari -15 + (-12:3) adalah ….
Penyelesaian:
Perhatikan pada soal ini -15 + (-12:3), ada operator tanda kurung, pembagian dan penambahan. Serta terdapat bilangan bulat positif (3) dan bilangan bulat negatif (-15 dan -12). Sesuai aturan operasi hitung, operasi dalam tanda kurung yang harus dikerjakan pertama dan sifat asosiatif tidak dapat diterapkan.
-15 + (-12:3) = -15 + (-4) …….. (bilangan negatif dibagi positif hasilnya pasti bilangan negatif)
– 15 + (-4) = -15 – 4 = -19 ……. (penambahan dua bilangan negatif)
Hasil dari 30 – (7x(-5)) adalah
Penyelesaian:
Ini juga mudah, perhatikan soal 30 – (7x(-5)) terdapat tanda kurung dalam tanda kurung serta terdapat operator perkalian dan pengurangan. Bilangan bulat positif yaitu 30 dan 7 serta negatif adalah -5. Oleh karena itu, pertama kita proses mulai dari yang dalam kurung.
30 – (7x(-5)) = 30 – (7 x -5) = 30 – (-35) …….. (Operator pengurangan dikalikan dengan bilangan bulat negatif, hasilnya positif)
30 – (-35) = 30 + 35 = 65
Hasil dari 27 : (-3) + (-14) adalah
Penyelesaian:
Soal ini pun mudah. Perhatikan soal ini 27 : (-3) + (-14), dapat kita lihat terdapat operator pembagian dan penambahan. Bilangan positif adalah 27 sementara negatif adalah -3 dan -4. Operator tertinggi adalah pembagian.
27 : (-3) + (-14) = – 9 + (-14) = -9 – 14 = -23
Hasil dari 14 + (6: (-2) x 3 + 1) – (2 x 24 : 8 – 12) adalah
Penyelesaian:
Soal diatas terdiri atas 3 bagian yaitu bagian paling sederhana ada satu (14) dan dua bagian tanda kurung yang dipisahkan oleh operator pengurangan. Kedua operator tanda kurung tersebut mengandung berbagai operasi didalamnya, mulai dari perkalian, pembagian, pengurangan dan penambahan. Sesuai hukumnya, proses yang tanda kurung pertama, dan didalam tanda kurung, dahulukan proses perkalian dan pembagian mulai dari bagian kiri ke kanan.
14 + (6: (-2) x 3 + 1) – (2 x 24 : 8 – 12) = 14 + (6:-2 x 3 + 1) – (2 x 24 : 8 – 12)
= 14 + (-3 x 3 + 1) – (48 : 8 – 12) = 14 + (-9 + 1) – (8 – 12)
= 14 + (-8) – (-4) = 14 – 8 + 4 = 10
Nilai y pada 8y x 2 : 12 = 8 adalah
Penyelesaian:
Ini juga mudah karena merupakan persamaan dengan satu variabel. Apalagi operator matematika yang digunakan hanya perkalian dan pembagian. Caranya kita selesaikan kedua sisi persamaan.
8y x 2 : 12 = 8
bentuk lainnya sama saja dengan
8 x y x 2 : 12 = 8
16y:12 = 8
16y = 8 x 12
16y = 108
y = 108/16 = 6,75



